atomic puzzles 1For a concurrency course I'm co-teaching, I came up with a few puzzles about C++ memory order and atomics.
I figured this is good material for a technical blog, so here we can discuss one such classic puzzle demonstrating load buffering! As a bonus, we will also peek into the differences between operational and axiomatic memory models, and how that makes things really painful when it comes to teaching this black magic voodoo.
I will assume you're familiar with the C++ memory model. In particular:
I might write my own blog post at some point explaining all the jargon at some point, but I won't go into it here. If you were confused by the above jargon, then these puzzles are not for you yet.
In the following puzzles,
the question is about what the possible return values of main() are.
int main() {
atomic_int x{0}; atomic_int y{0};
int read_x = 0; int read_y = 0;
thread t1{[&]() {
read_x = x.load(acquire); // RX
y.store(1, release); // SY
}};
thread t2{[&]() {
read_y = y.load(acquire); // RY
x.store(1, release); // SX
}};
t1.join(); t2.join();
return read_x + read_y;
}Take your time to read the code snippet above. The remaining puzzles are all variations of it.
This first one is a classic demonstration of release-acquire synchronization.
The possible return values are 0 and 1.
These are both obviously possible.
0 may be observed whenever both loads completely execute before either store occurs,
and 1 may be observed when the two threads execute serially, for example.
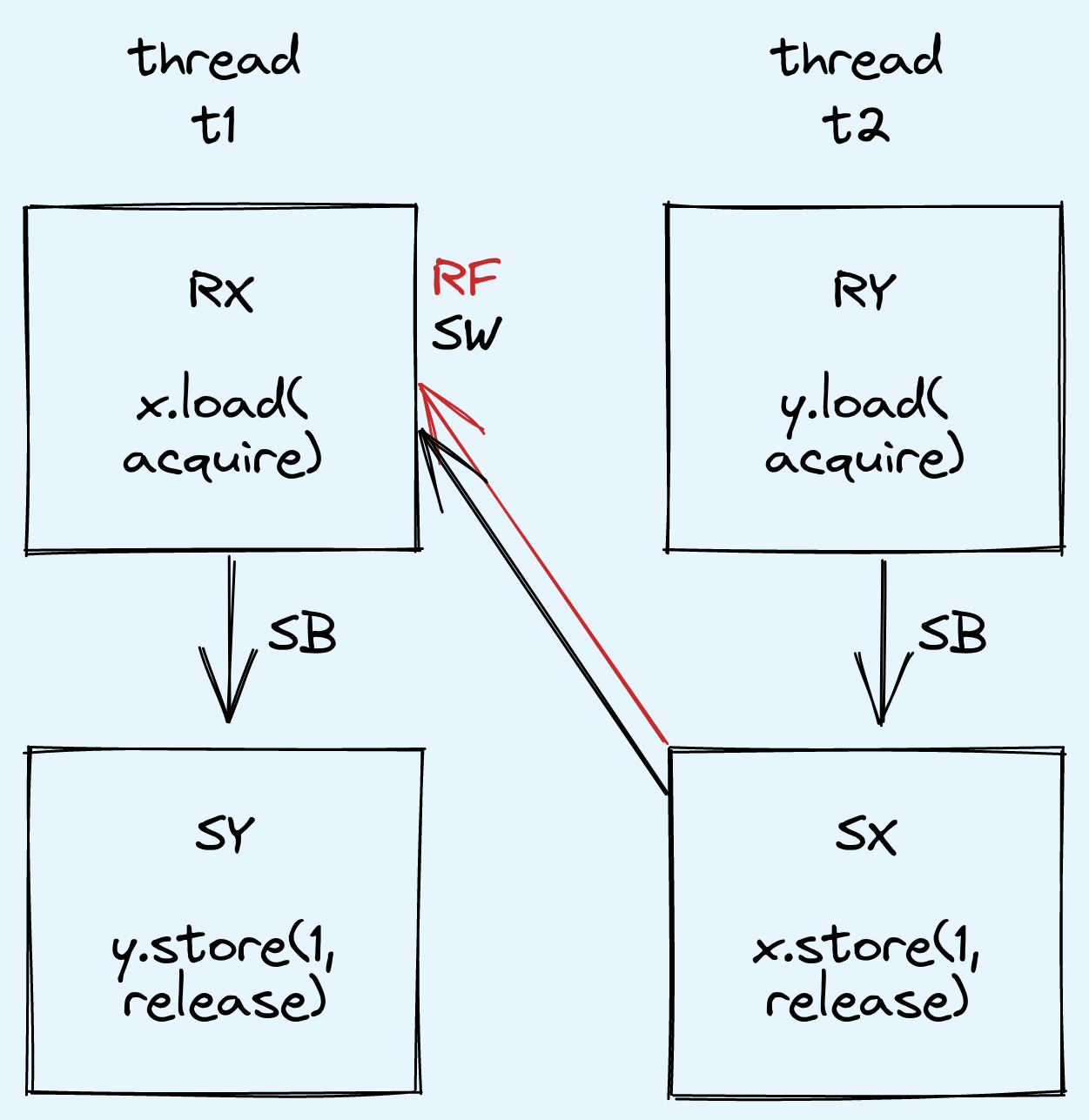
2 is not possible because for that to happen,
both read_x and read_y must be 1.
Making this assumption will allow us to reach a contradiction.
In particular, assume that x.load(acquire) returned the value that x.store(1, release) stored.
This establishes a synchronizes-with relationship between the release and the acquire,
and thus we have the following happens-before relationships:
By transitivity, we have the the following relationship in particular:
read_y = y.load(acquire); happens-before y.store(1, release);Now, by read-write coherence,
y.load(acquire) (RY) is not allowed to return the value written by y.store(1, release); (SY),
and instead must be an older value preceding that store in the modification order of y.
This older value can only be the initial value 0.
We assumed that read_x == 1 and deduced that read_y == 0 must have happened.
Thus, there is no way for both reads to return 1 and main() cannot return 2.
We can sum up the relationships in the following diagram:

In this next puzzle, we turn one of the loads into a relaxed load.
int main() {
atomic_int x{0}; atomic_int y{0};
int read_x = 0; int read_y = 0;
thread t1{[&]() {
read_x = x.load(relaxed); // RX, This is now relaxed
y.store(1, release); // SY
}};
thread t2{[&]() {
read_y = y.load(acquire); // RY
x.store(1, release); // SX
}};
t1.join(); t2.join();
return read_x + read_y;
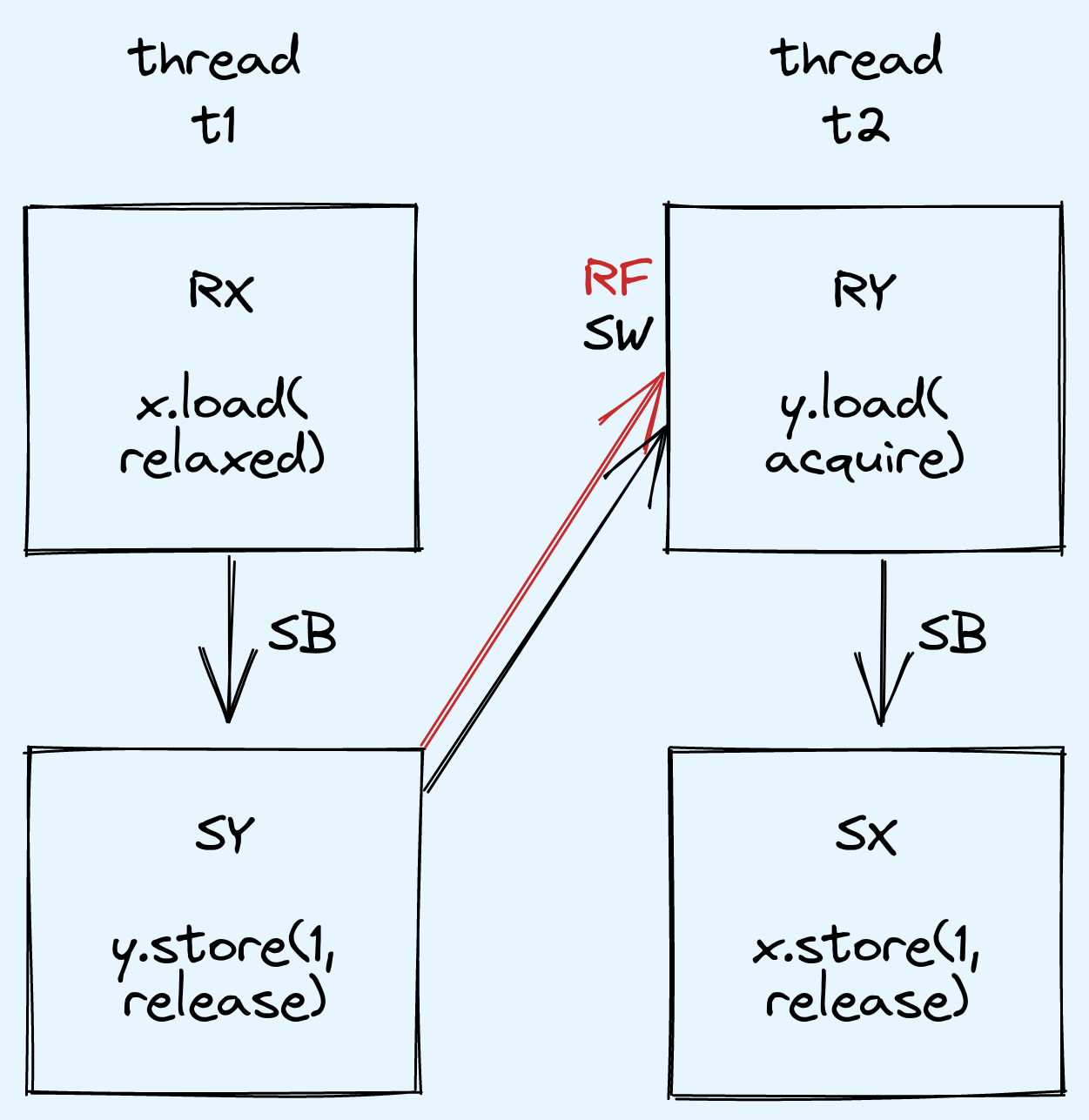
}Many students focus too much on the relaxed load, and are tricked into saying that a return value of 2 is possible.
I imagine that students have the following picture in their heads:
1 in x.1.
However, because the load is relaxed, there is no synchronizes-with relationship.synchronizes-with relationship between the two threads,
RY may return any value in the modification order of y,
and in particular, it may return 1.This logic suffers from the inverse error.
Simply because x no longer provides the synchronizes-with relationship
does not mean that the two threads are unordered.
In this case, it suffices to use the exact same proof as we did for Puzzle 1,
but apply the reasoning on read_y instead of read_x.
Assuming read_y == 1, we will be able to show that read_x == 0,
and thus main() cannot return 2.
In this puzzle, we make EVERYTHING relaxed.
int main() {
atomic_int x{0}; atomic_int y{0};
int read_x = 0; int read_y = 0;
thread t1{[&]() {
read_x = x.load(relaxed); // RX, This is now relaxed
y.store(1, relaxed); // SY, This is now relaxed
}};
thread t2{[&]() {
read_y = y.load(relaxed); // RY, This is now relaxed
x.store(1, relaxed); // SX, This is now relaxed
}};
t1.join(); t2.join();
return read_x + read_y;
}Some students have trouble with this puzzle as they intuitively use a sequentially consistent model of execution, even though that's not the case in reality.
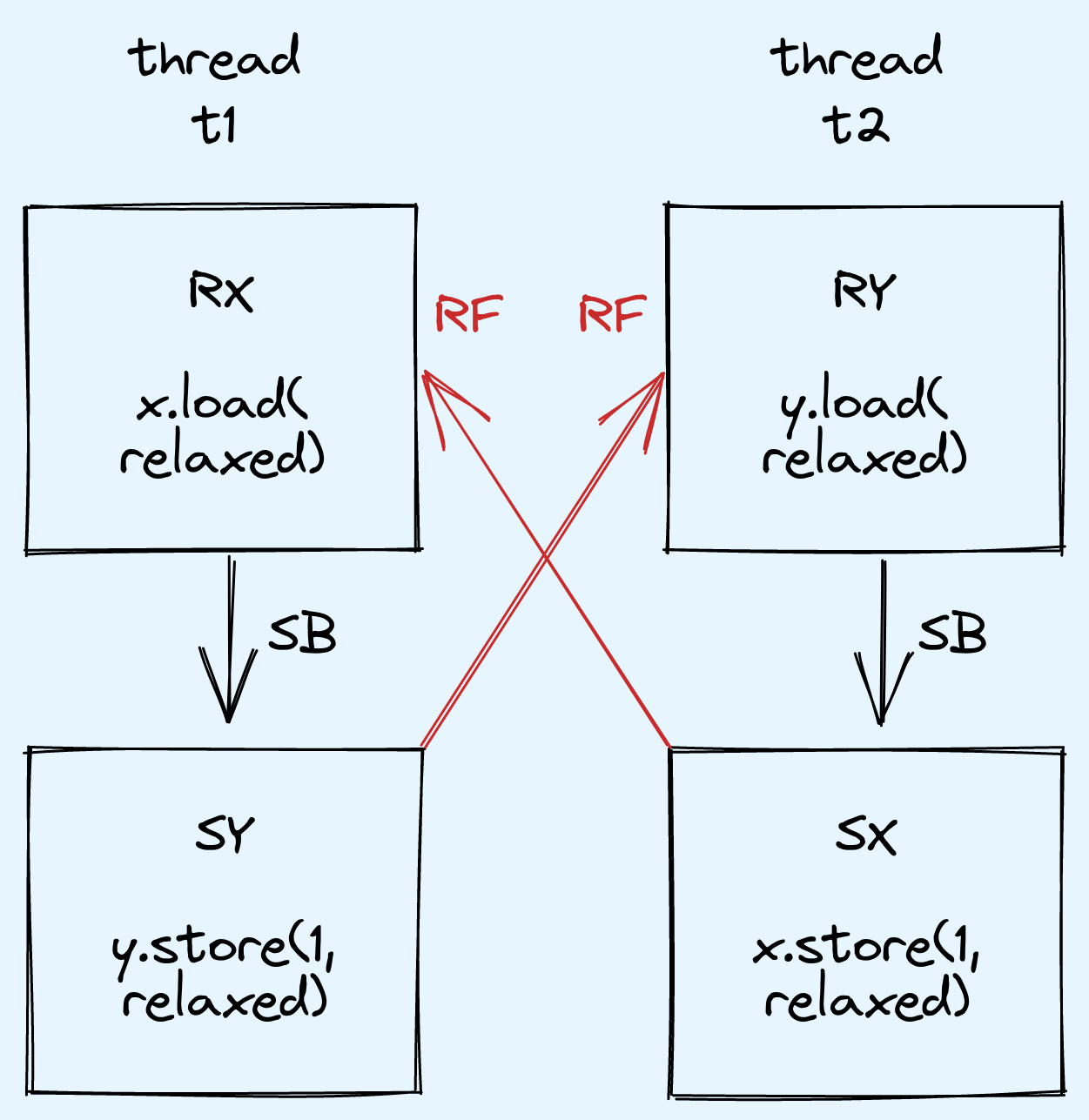
In this case, main() may return 2.
This is surprising as it means that both loads read their value from the opposite thread's store,
even though it feels like "one of the reads must have happened before either store can start".
One way to intuitively explain this is with reordering. (Note that I personally do not like such explanations.) Since RX and SY are both relaxed operations to different atomic variables, the compiler is allowed to reorder RX after SY, resulting in the following "optimized code":
thread t1{[&]() {
y.store(1, relaxed); // Compiler did some reordering?
read_x = x.load(relaxed);
}};While this might be possible due to some advanced analysis of the variables, a slight modification to the program would make this optimization invalid:
extern atomic_int& x; // Reference defined in a different translation unit
extern atomic_int& y; // Reference defined in a different translation unit
int main() {
int read_x = 0; int read_y = 0;
thread t1{[&]() {
// Here, we don't know if x and y alias each other!
read_x = x.load(relaxed);
y.store(1, relaxed);
}};
thread t2{[&]() {
// Same here
read_y = y.load(relaxed);
x.store(1, relaxed);
}};
t1.join(); t2.join();
return read_x + read_y;
}Now, it is possible that x and y both reference the same atomic_int.
Reordering RX and SY here is no longer allowed as doing so would break read-write coherence.
But even if the compiler is not allowed to reorder RX and SY in the general case,
the compiler is not required to prevent the processor from doing so
in the case that x and y are different.
Indeed, on the ARMv8 architecture,
its weaker memory model allows this "reordering" to occur due to load buffering.
Focusing on the first thread t1, load buffering (and store buffering) occurs here when both the store (SY) and load (RX) instructions are issued and processing starts concurrently. They may complete in any order, so it is possible the store (SY) completes first.
Now imagine the same happens on the other thread,
and the resulting side-effects of both stores (SY and SX) are visible to both threads immediately.
The loads (RX and RY) now complete, and they both read the new value 1.
Note that in this explanation, we singled out one particular architecture (ARMv8)
and showed what could've happened to result in 2 being observed.
However, it is harder to explain why 2 is allowed by C++.
As such, I generally recommend against such explanations,
but they are still useful in specific cases as a way to help motivate the C++ memory model's design.
Above, we used "reordering" to explain how some behaviour could have been observed. In the next puzzle, we will soon see some behaviour that's allowed by C++, but is unfortunately not easy to understand with an operational mental model.
We are about to enter voodoo territory, so let's pause here to explain what I mean by an operational or axiomatic memory model.
When it comes to memory models, an operational model is one that tries to explain all possible behaviours by defining an abstract machine that executes code. This abstract machine is nondeterministic, so there are many possible executions. Here, all executions are forbidden unless it is possible for this abstract machine to do it.
On the other hand, an axiomatic model is one that tries to explain all forbidden behaviours by defining a set of axioms that must be satisfied. Alternatively, you could also view it as a set of guarantees, since a guarantee is simply a statement that breaking it is forbidden. Here, all executions are allowed unless it is forbidden, i.e. it breaks some guarantees.
Operational models are generally preferred by people as they are intuitive. If C++ used an operational model, then whenever we write some code, all we need to do is to execute it in our heads to figure out what the result is.
But axiomatic models are easier to work with when it comes to program analysis as they are much easier to use in a formal proof. Sometimes (but not always), program transformations and optimizations are easier to prove sound with an axiomatic model.
It is an active area of research to find equivalent pairs of axiomatic and operational models. Having such pairs would allow us to use whichever model we find most convenient, which is great!
Going back to the puzzles, while the load buffering explanation works, it is one that works on operational models of atomics. However, the C++ memory model is defined axiomatically. While this would not really be an issue if we can find an equivalent operational model, I don't currently know of one yet.
In this final puzzle, we turn both loads into relaxed loads, but keep the stores as release stores.
int main() {
atomic_int x{0}; atomic_int y{0};
int read_x = 0; int read_y = 0;
thread t1{[&]() {
read_x = x.load(relaxed); // RX, This is now relaxed
y.store(1, release); // SY
}};
thread t2{[&]() {
read_y = y.load(relaxed); // RY, This is now relaxed
x.store(1, release); // SX
}};
t1.join(); t2.join();
return read_x + read_y;
}This is the example I show to students to explain why
a reordering-based operational mental model of C++ atomics
is difficult to create when it comes to edge cases like these.
When thinking in terms of reordering, it is tempting to say that neither RX nor RY
can be reordered after SY or SX in their respective threads, as they are release stores.
This leads us into thinking that main() cannot return 2.
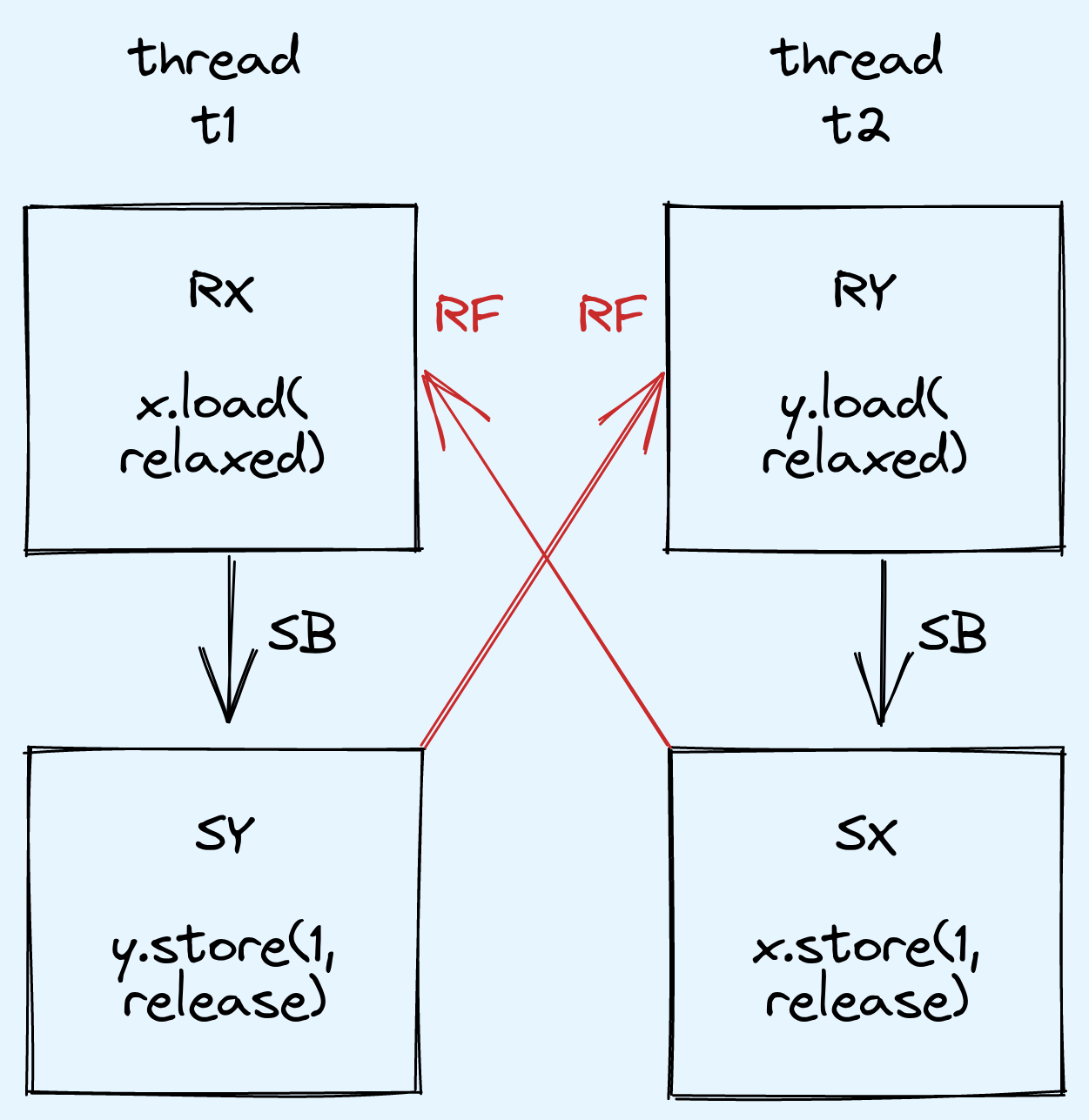
This conclusion is wrong. In fact, main() IS allowed to return 2.
As neither load is an acquire, we still have no synchronizes-with relationship between the two threads. There is still nothing in the C++ specification forbidding both loads from reading from their respective stores in the opposite thread.
This is counterintuitive as it seems like some kind of time travel has occurred.
If both loads read a value of 1, then it means that both stores have already been executed.
But loads cannot be reordered after either release, so load buffering does not really apply here.
Indeed, on both the x86 and ARM architectures, the code above will never return 2,
as load buffering (as implemented on ARM) is not allowed to cross a store-release.
To fit load buffering to the C++ memory model, one way is to allow it to cross a store-release as long as it still completes before the corresponding load-acquire, but I'm not sure if this weakening of the ARM memory model is entirely correct.
Unfortunately, I don't have a satisfying explanation for this behaviour. At the end of the day, all I can say is that this is a possible execution, and there is nothing in the C++ specification that forbids this.
I think that many people prefer using a reordering mental model as it is sometimes easier
to explain why certain behaviours are possible by saying what transformations are allowed,
and it becomes easy to explain things like why main() may return 2 in Puzzle 3.
On the other hand, it's not very satisfying to say,
"I read the entire C++ specification, and there was nothing in it that said this was not allowed."
However, as we can see, sometimes a gap between more intuitive operational models and axiomatic models like C++'s exists, and this can result in behaviour that's not easy to explain with either kind of model.
Personally, I think it's good to learn the C++ memory model simply because it is what the language guarantees and the wording is clear and precise. Ideally, we want to write code that works on all targets conforming to the C++ memory model, even if there are some behaviours (e.g. Puzzle 4) that won't be observed on current hardware.
It is possible that some future or esoteric hardware breaks some of the additional assumptions we like to make (e.g. loads cannot be reordered past a store-release). These targets might still technically conform to the C++ memory model, but our code might not execute correctly.
If such hardware becomes available, I hope that these operational models are either weakened to match C++, or that the C++ memory model is strengthened to match the operational models (at performance cost on such hardware).